The Many-Body Quantum Field Theory tries to solve the Many-Body problem following this way:
First it lets aside the many-body wavefunction (who cares about knowing the probability to observe a particular configuration in which the N particles are exactly in those N positions - a point already made by statistical mechanics). Then, changing completely the mathematical framework, it proceeds for a Second Quantization of the theory toward the construction of a Quantum Field Theory for the Many-Body interaction. At the end, the problem is reformulated not any more in term of a complex many-body wavefunction, but, rather, condensed in term of a more treatable Green Function or Propagator of the system, containing just only the interesting and macroscopically observable informations, that is: the total energy of the system as well as all the other expectation values of observables of the system; and the excitation spectrum.
In principle the Green Function and all the observables can be calculated perturbatively in the many-body interaction. And in fact the first order of the Many-Body Perturbation Theory (MBPT) gives back the Hartree-Fock approximation (a good check to verify that old results could be reobtained by a more complete theory), while the second gives the Born approximation. Unfortunately, the coupling constant upon which the theory is expanded is not small, which do not guarantee that further orders are less important than firsts.
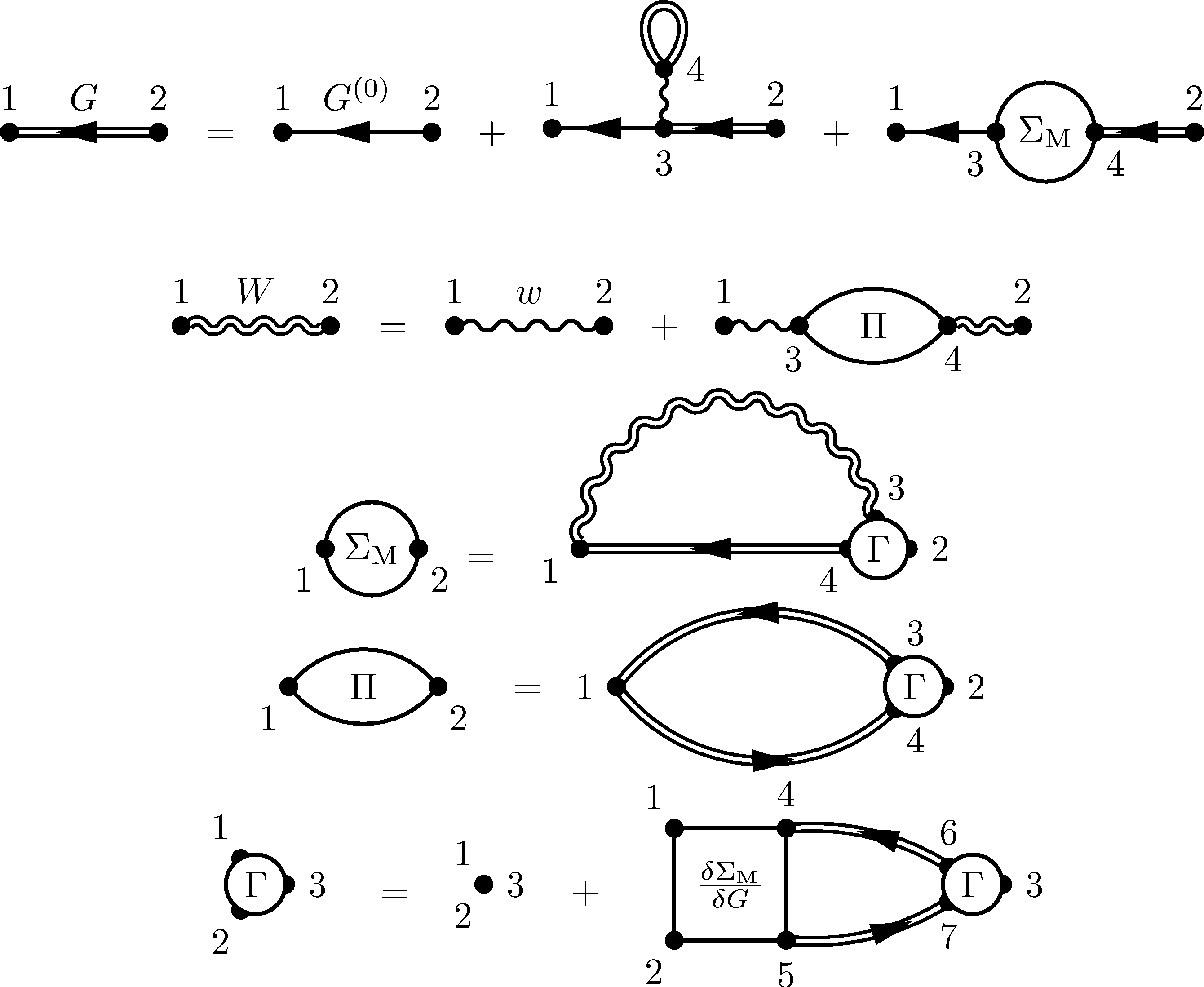
However, a very elegant, iterative in contrast to perturbative, approach has been set up for the theory: that one of the Hedin Equations, a set of 5 integro-differential equations to be solved self-consistently starting from the perturbative 0 order, or from Hartree-Fock or from any other reasonable aproximation (DFT-LDA) for instance). We present here in Feynman diagrammatic form the set of these equations which can be derived using a perturbative or also a more elegant functional approach.