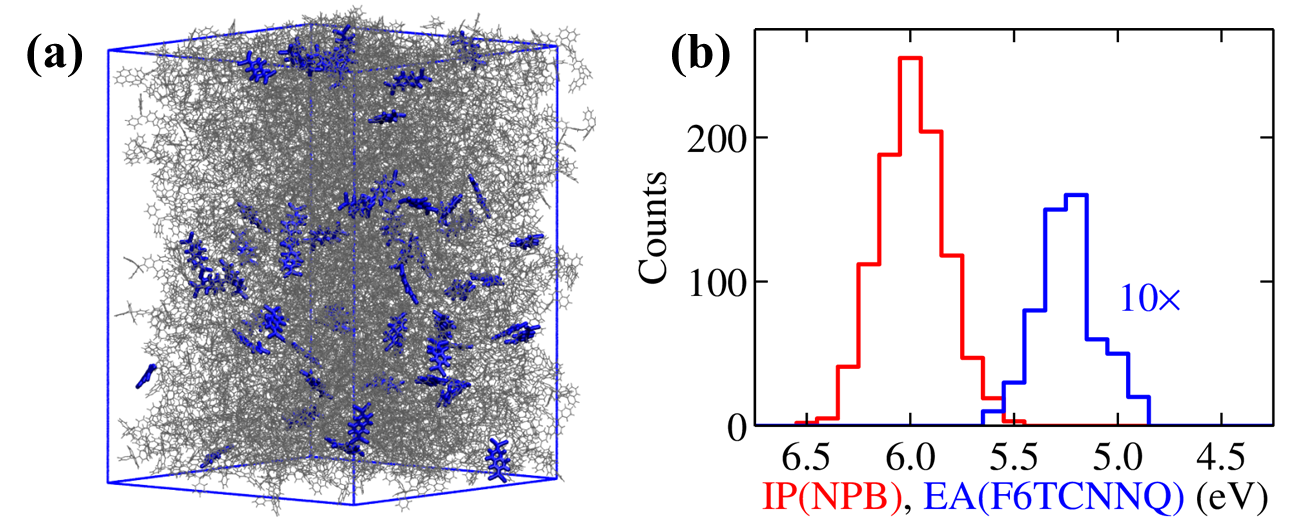
Quasiparticle (GW) electronic properties calculated for (a) a realistic amorphous morphology of molecular NPB (wireframe representation) doped with F6TCNNQ (blue sticks) at 5% concentration. Distributions of (b) IP of NPB (IPS) and EA of F6TCNNQ (EAD) for the molecules in the sample. These calculations have been obtained with embedded QM/MM GW calculations performed with the Fiesta/Mescal package.
["Host dependence of the electron affinity of molecular dopants", Jing Li, Ivan Duchemin, et al., Mater. Horiz., 2019, 6, 107-114].

Schematic representation of the dynamic solvent induced shifts for the pi-pi* excitation in acrolein, the CT excitation in the benzene-TCNE complex, and the (planar) PNA mixed excitation. The embedded BSE/GW+PCM shift of the excitation energies is compared to the sum of the "linear response" and "state specific" contributions calculated at the TD-DFT/PCM (PBE0 functional) level. These calculations have been obtained with embedded BSE/GW+PCM calculations performed with the Fiesta package.
["The Bethe-Salpeter Formalism with Polarisable Continuum Embedding: Reconciling Linear-Response and State-Specific Features", Ivan Duchemin, Ciro Achille Guido, Denis Jacquemin and Xavier Blase, Chem. Sci., 2018, 9, 4430-4443]
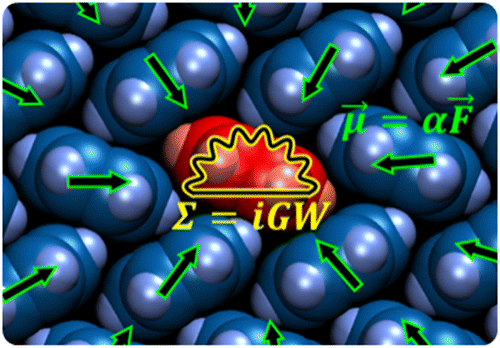
Symbolic representaton of the QM/MM implementation of the GW formalism, combining the Fiesta (QM) code with the Mescal (MM) discrete polarizable model with induced charges and dipoles. It can be shown that the properties of bulk semiconductors can be well reproduced in the present QM/MM formalism that properly includes electrostatic and polarization effects originating from the environment and that strongly renormalize the bulk band structure as compared to gas phase molecular properties. [Combining the Many-Body GW Formalism with Classical Polarizable Models: Insights on the Electronic Structure of Molecular Solids, J. Li, G. D'Avino, I. Duchemin, D. Beljonne, and X. Blase, J. Phys. Chem. Lett. 7, 2814 (2016).]
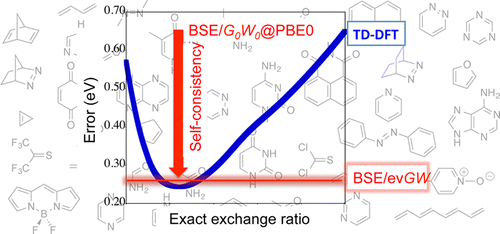
Accuracy of the Bethe-Salpeter formalism as compared to TD-DFT calculations (global hybrid
functionals) for the so-called Thiel's set of molecules. The blue line indicates the mean absolute error on a hundred
transition energies corresponding to TD-DFT calculations with global hybrid functionals with increasing amount of exact
exchange (minimal error at about 25% of exact exchange as in the PBE0 functional). The error is calculated taking as reference
cc-pVTZ CC3 calculations. While BSE calculations starting from non-self-consistent G0W0@PBE0
quasiparticule energies yields too small excitations energies for this set of "small" molecules, BSE calculations on top of
a simple evGW@PBE0 calculations with partial self-consistency on the eigenvalues offer a similar accuracy as compared to the
best TD-DFT results.
[Editor choice open-access: "Benchmarking the Bethe-Salpeter Formalism on a Standard Organic Molecular Set", D. Jacquemin, I. Duchemin, X. Blase, J. Chem. Theory Comput. 2015, 11, pp 3290-3304.]
Link to paper
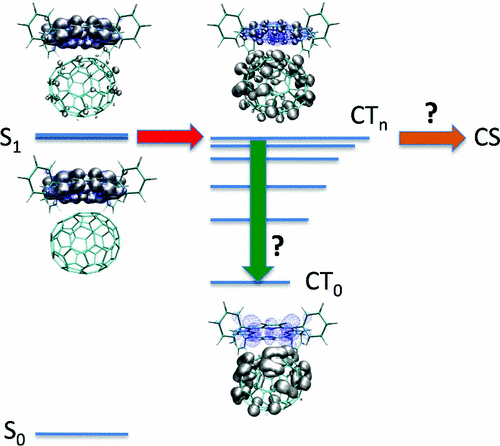
Symbolic representation showing the potential flow of transitions from intramolecular
(Frenkel) excitations, localized on the donor, to resonant hot charge-transfer (CTn) states (red arrow) and subsequently
unbound charge-separated (CS) electron-hole pair (orange arrow) in a C70/zinc-tetraphenyl-porphyrin complex.
The adverse decay into the low-lying CT0 state is also represented with the green arrow.
The Bethe-Salpeter excitonic eigenstates are represented as isocontours for the
(hole-averaged) electron distribution ((grey) and the (electron-averaged) hole distribution (blue).
["Resonant hot charge-transfer excitations in fullerene-porphyrin complexes: Many-body Bethe-Salpeter study", by Ivan Duchemin and Xavier Blase, Phys. Rev. B 87, 245412 - Published 10 June 2013].
